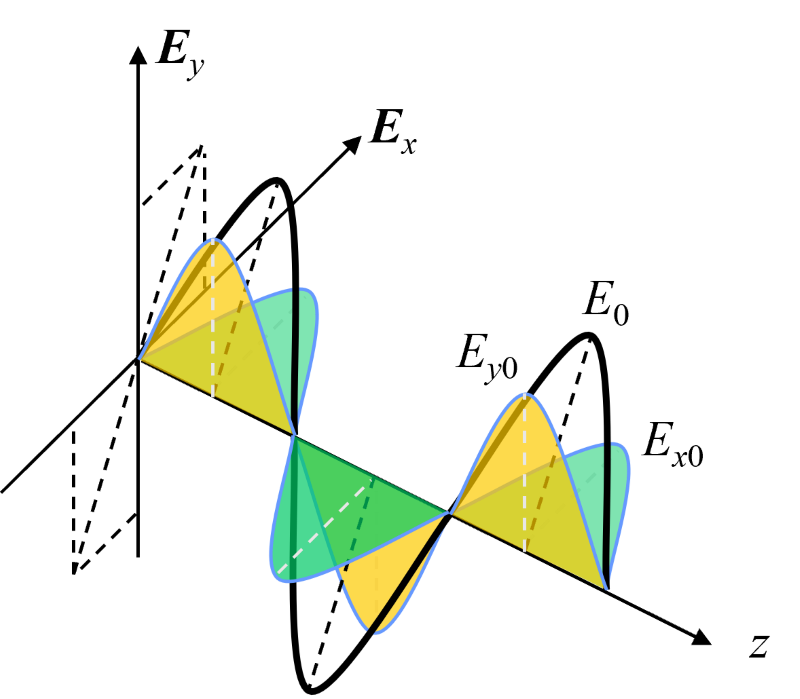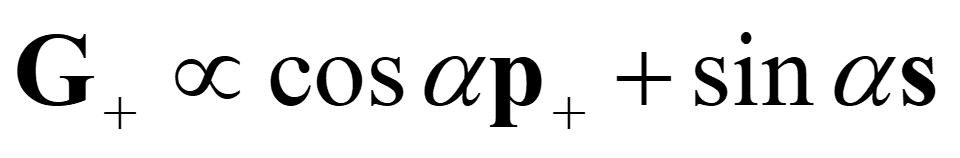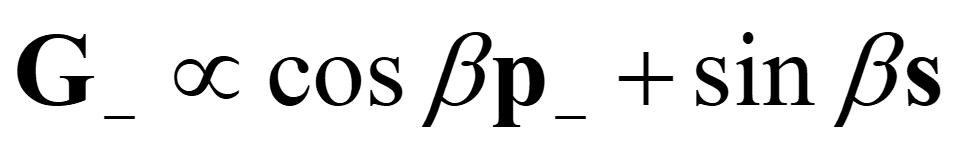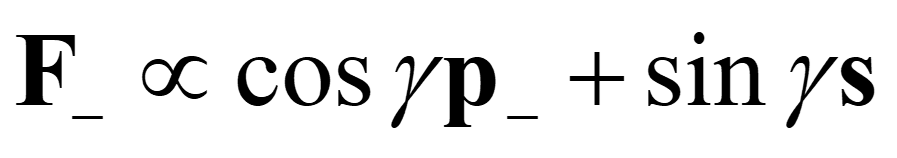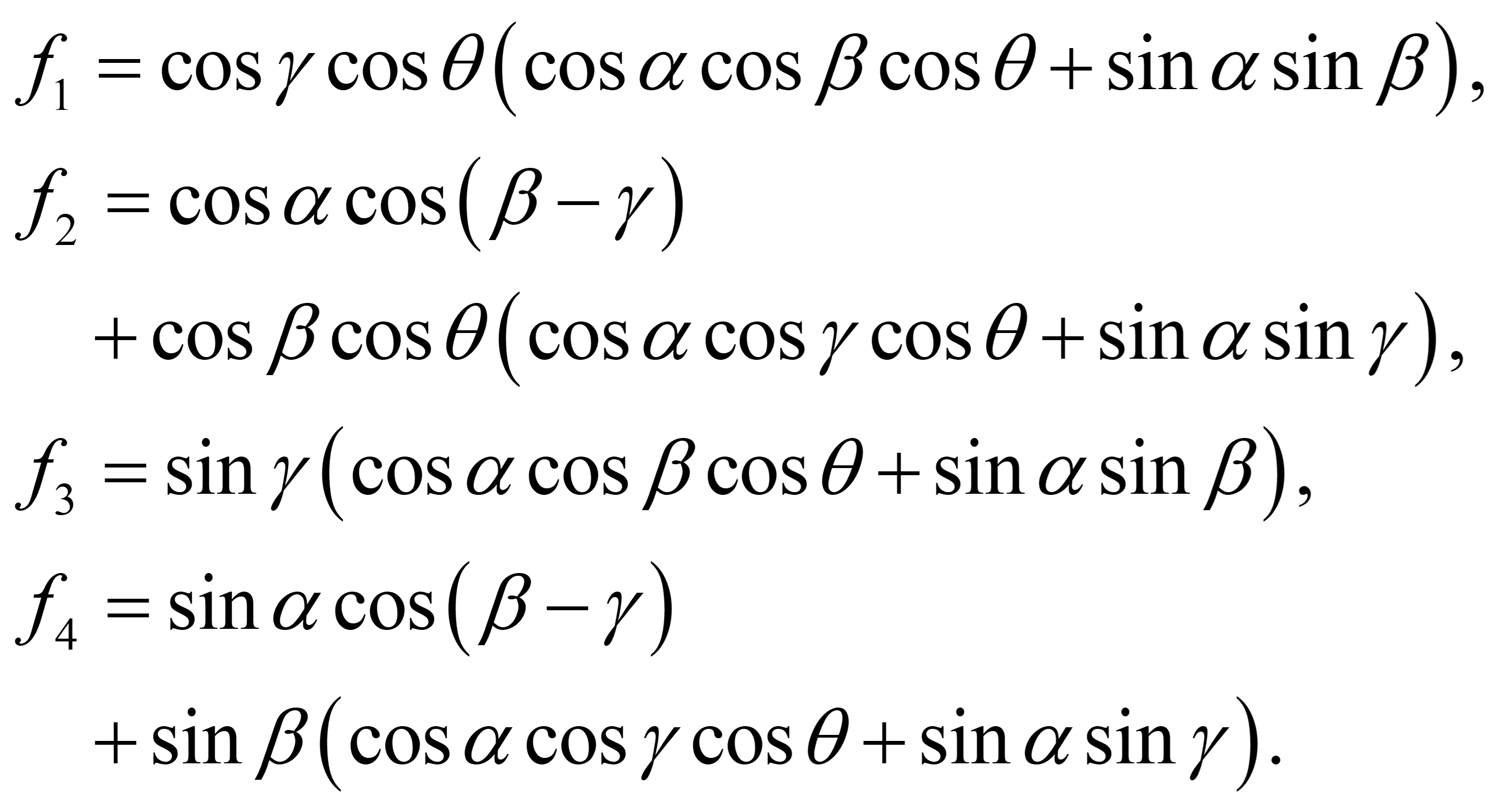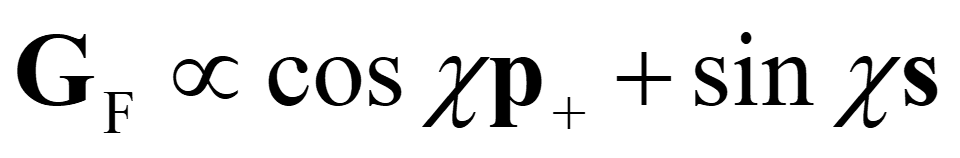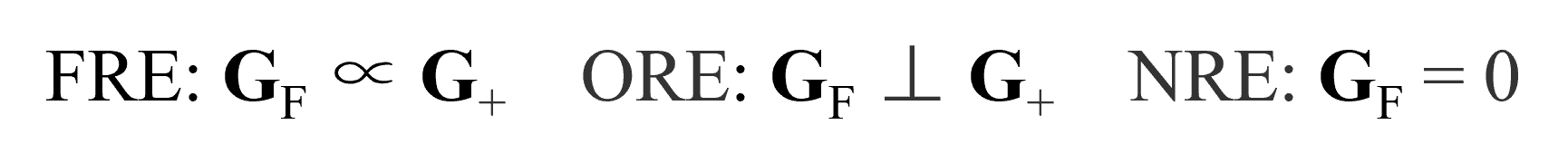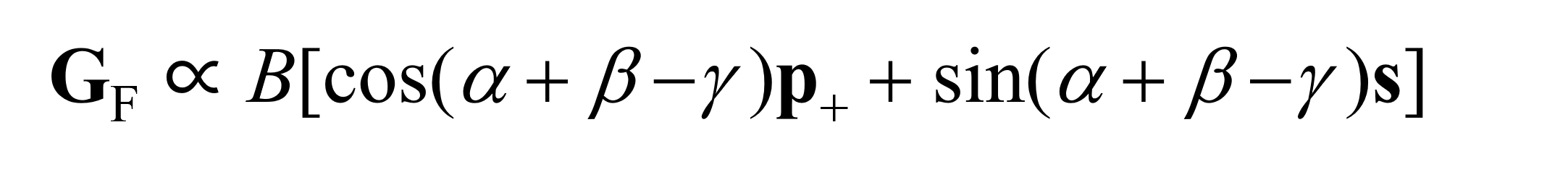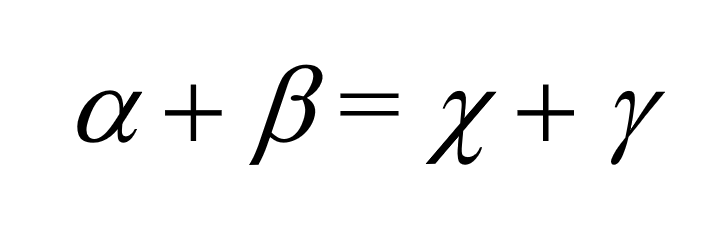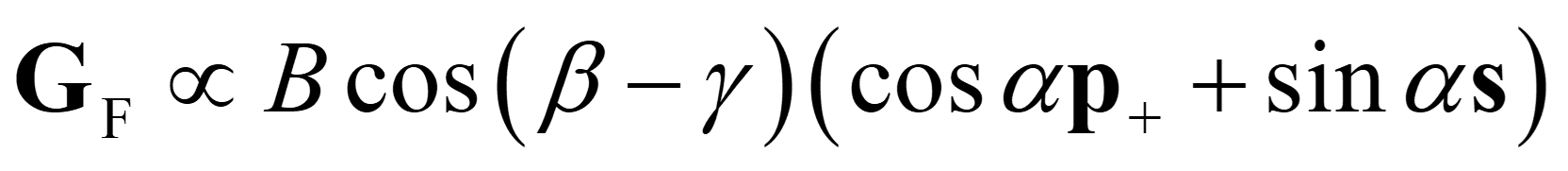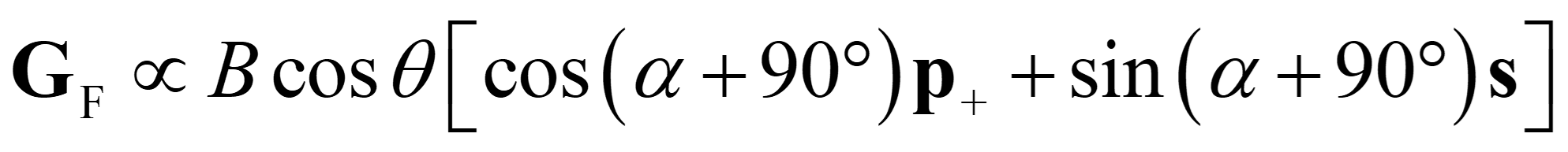| | |
偏振是光波的特性之一,当我们迎着光波的传播方向观察,描述光波的电矢量振荡是沿着一条直线的,我们称该光波的偏振态为线偏振光,线偏振态也是光波偏振态的最基本形式,任何形式的偏振态均可通过两个正交的线偏振态的叠加合成,如图1 所示的 Ex 和 Ey 。因此开展线偏振光的偏光全息研究就显得尤为重要。
|
|
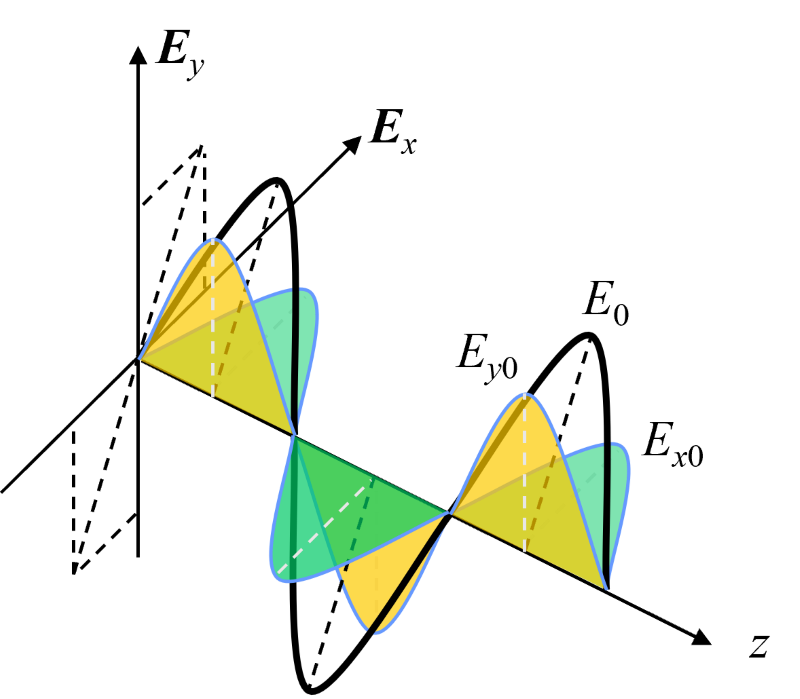
|
|
|
图1. 线偏光波可分解为两个正交的基矢方向振动的线偏振光波
|
|
|
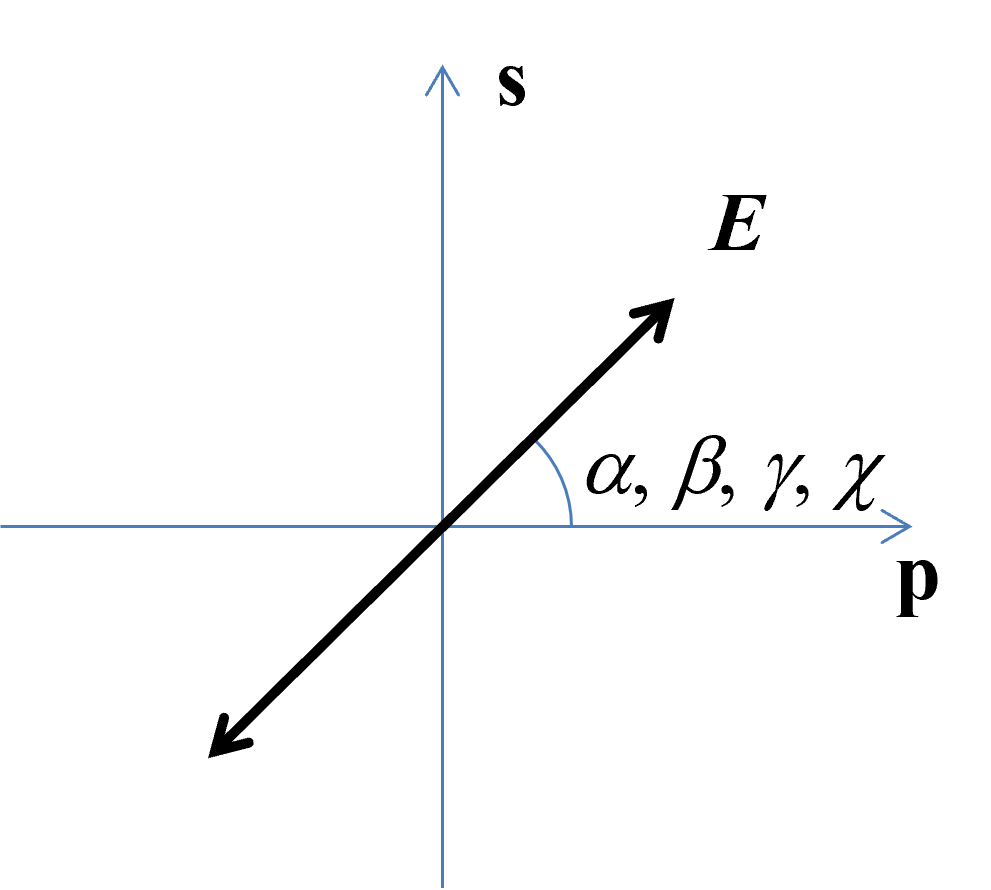
为了便于描述以及寻找最为直观的实验规律,通常定义 p 偏振(相当于 Ex 方向)和 s 偏振(相当于 Ey 方向)作为正交基矢量,它们同时垂直于波矢 k (沿 z 方向,其数值为 k = 2p/l)。定义线偏振光电矢量 (E) 的偏振角为 E 矢量与 p 矢量的夹角,如图2 所示。
|
|
|
|
|
图2. 线偏振光的基矢量与偏振角的定义
|
|
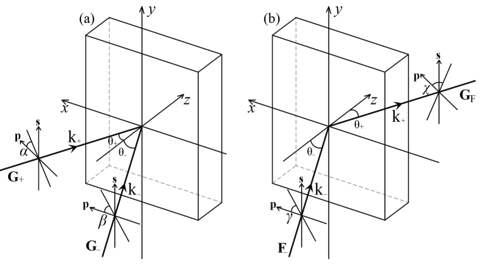
线偏振光的偏光全息在记录和再现过程中的各矢量的相互关系模型如图3 所示,此时,两个基矢量与 (x-y-z) 坐标系的关系如下:
|
|
p 偏振:线偏振的电矢量振动面平行于入射面,一般在 (x-z) 面内,显然,信号光与参考光的 p 偏振方向是不同的,分别用 p+ 和 p- 表示;
|
|
s 偏振:线偏振的电矢量振动面垂直于入射面,一般与 y 轴同方向,因此, s 偏振只有一个。
|
|
|
|
|
图3. 线偏振光的偏光全息的 (a)记录和 (b)再现模型
|
|
在记录过程中,线偏振的信号光(G+,偏振角为 α)和线偏振的参考光(G-,偏振角为 β)以 θ(θ = θ++θ-)的夹角进行干涉。用偏振敏感的介质记录三维的干涉光场分布,生成偏光全息图。在再现过程中,使用满足 Bragg 再现条件的线偏振读取参考光(F-,偏振角为 γ)照射偏光全息图,这些线偏振光的表达式分别如下:
|
|
|
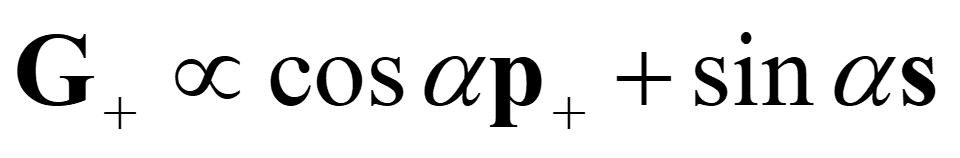
|
(1) |
|
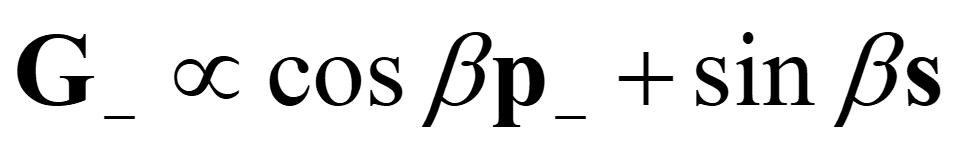
|
(2) |
|
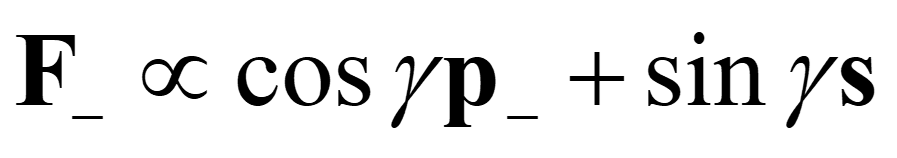
|
(3) |
|
按照张量的偏光全息理论,基于公式(1)-(3) 的定义,再现光场的表达式可写为:
|
|
|

|
(4) |
|
其中 fj (j = 1, 2, 3, 4) 分别表示为:
|
|
|
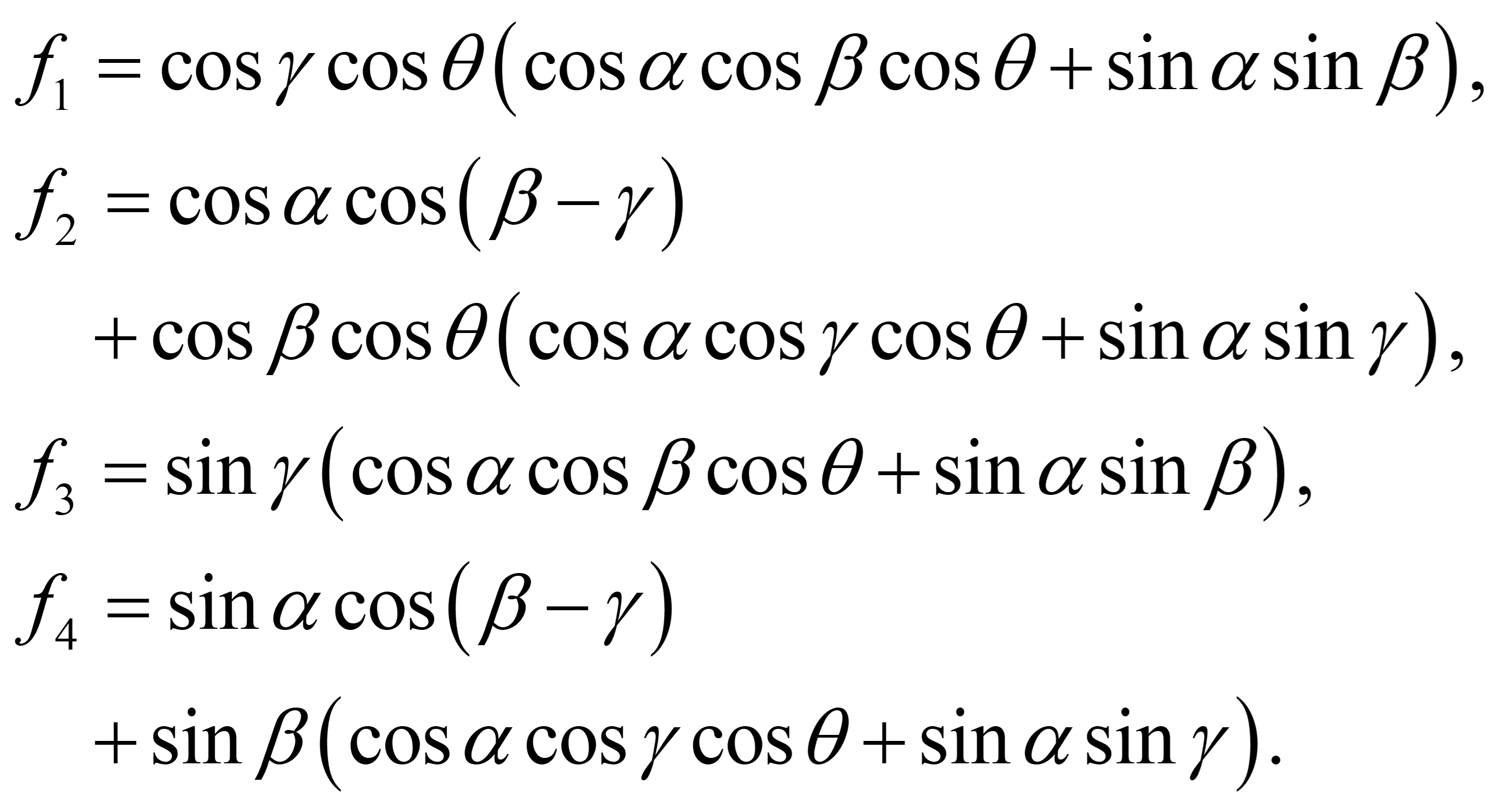
|
(5) |
|
|
从公式(4) 和公式(5) 可以看出,再现光(GF)仍为线偏振光,前期的实验结果也验证了这一点。因此,可以用同样的形式定义再现偏振光(GF,偏振角为 χ)如下
|
|
|
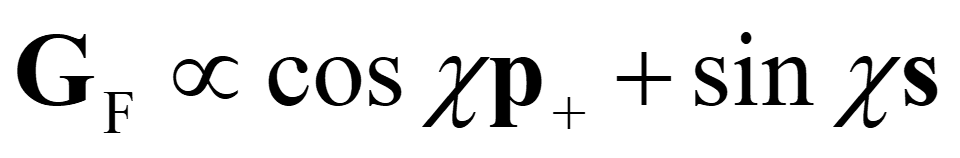
|
(6) |
|
再现偏振光的结果表明,一般情况下,再现光的表达式比较复杂,再现光的振幅和偏振角受到信号光、记录参考光、读取参考光的偏振角以及干涉角的约束,同时也受到强度响应系数 A 和偏振响应系数 B 的调控。A 和 B 这两个系数(参照偏光全息理论)均由材料的光学性质、记录时曝光能量和时间来决定,其比值 (A/B) 为曝光响应系数。
在讨论线偏振光的偏光全息再现特性之前,先介绍几个与偏光全息相关的再现现象。分别是:
|
忠实再现:FRE (Faithful Reconstruction Effect),再现光的偏振矢量与信号光完全一致,
在线偏振光的偏光全息中,就是再现光的偏振角与信号光的相同;
正交再现:ORE (Orthogonal Reconstruction Effect),再现光的偏振矢量与信号光矢量正交,
在线偏振光的偏光全息中,就是再现光的偏振角与信号光的相差90°;
零 再 现 :NRE (Null Reconstruction Effect),再现光的偏振矢量为零,即没有再现光。
以上偏光全息的三种再现现象的数学表述形式如公式 (7) 所示。
|
|
|
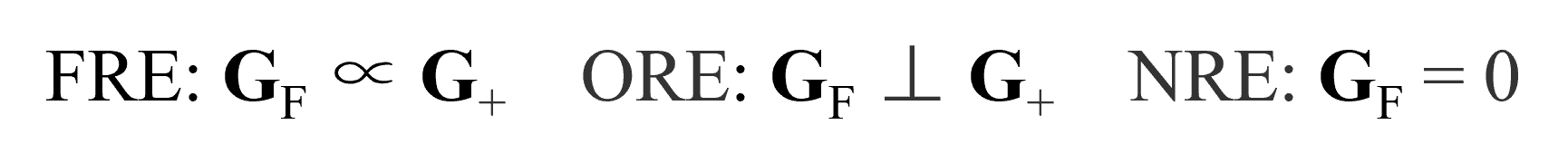
|
(7) |
|
首先,讨论干涉角为零(θ = 0)时,线偏振光的偏光全息再现特性。此时cosθ = 1。当记录的光强度和曝光时间满足一定的条件(A + B = 0)时,公式(4) 和公式(5) 可以简化为
|
|
|
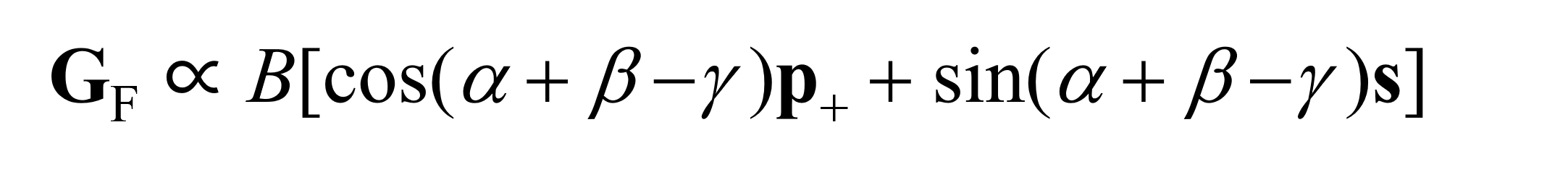
|
(8) |
|
公式 (8) 与 (6) 比较可得,α + β - γ = χ 正好是再现信号光的偏振角。因此得到
|
|
|
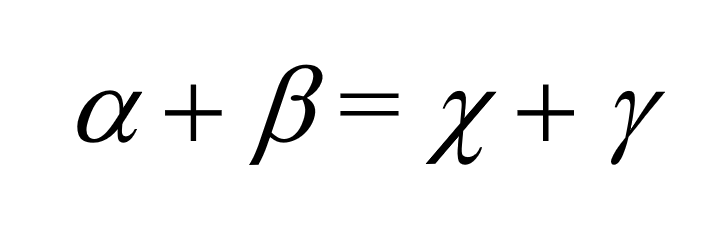
|
(9) |
|
公式 (9) 表明,线偏振光在偏光全息记录前后的信号光与参考光的偏振角之和是一个常数。这是一个非常有意义的结论。有关这个结论的计算和实验验证可参阅相关文献(Optics Express, 2021, 29(5), 6947)的介绍。
其次,讨论干涉角为直角(θ = 90°)时,线偏振光的偏光全息再现特性。此时cosθ = 0,当记录信号光、记录参考光和读取参考光中任何一束只有 p 偏振(α = 0°、β = 0° 或 γ = 0°)或偏光全息的记录满足一定曝光条件(A + B = 0)时,公式 (4) 和 (5) 可以简化为:
|
|
|
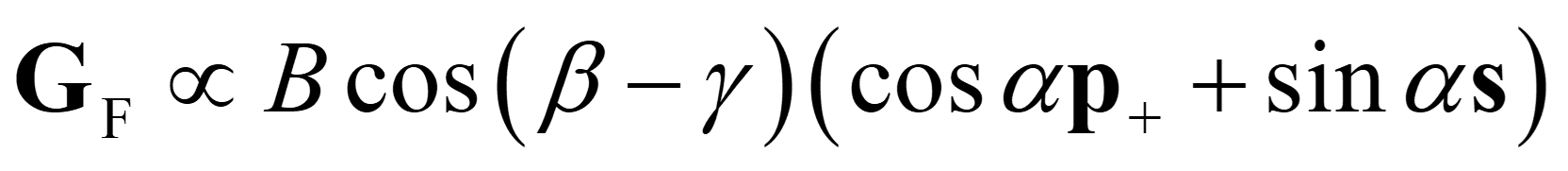
|
(10) |
|
公式 (10) 与 (6) 比较可知,再现信号光与记录信号光的偏振方向一致(χ = α ),实现了忠实再现。如果记录和读取参考光的偏振角相差 90° (β - γ = 90°) 时,会出现零再现。有关这个结论的计算和实验验证可参阅相关文献(Optics Letters, 2021, 42(7), 1377)的介绍。
再次,讨论干涉角为任意角(0 < θ < 90°)时,线偏振光的偏光全息再现特性。当偏光全息的记录满足一定曝光条件(A + B = 0)时,且记录和读取参考光的偏振角相同 (β - γ = 0°),公式 (4) 和 (5) 可以简化为:
|
|
|

|
(11) |
|
公式 (11) 与 (6) 比较可知,再现信号光与记录信号光的偏振方向一致(χ = α ),实现了忠实再现。如若记录和读取参考光的偏振角相差90° (β - γ = 90°) 时,公式 (4) 和 (5) 可以简化为:
|
|
|
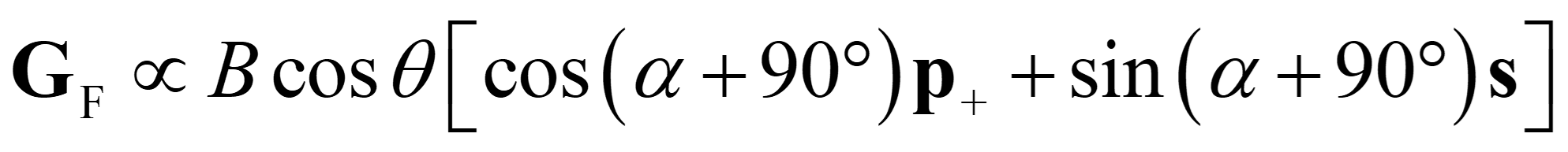
|
(12) |
|
公式 (12) 与 (6) 比较可知,再现偏振光与记录信号光的偏振角相差 90° (χ = α + 90°),互为正交关系。实现了正交再现。有关这个结论的相关计算和实验验证可参阅相关文献(Optical Review, 2015, 22, 829)和(激光与光电子学进展, 2021, 58(4), 0409001)的介绍。
最后,讨论曝光响应系数(A/B)。在前面讨论各种再现特性时,需要满足 A + B = 0 这个条件。如何获得这个系数(A/B)就显得特别必要。当记录和读取参考光均为 s 偏振时,可以从公式 (4) 和 (5) 获得曝光响应系数表达式
|
|
|

|
(13) |
|
从公式 (13) 可见,曝光响应系数(A/B)可通过测得再现光与信号光的偏振角来获得。与曝光响应系数相关的计算和实验验证可参阅相关文献(Optics Express, 2021, 29(9), 14033)和(Optics Letters, 2021, 46(19), 4789)的介绍。
|