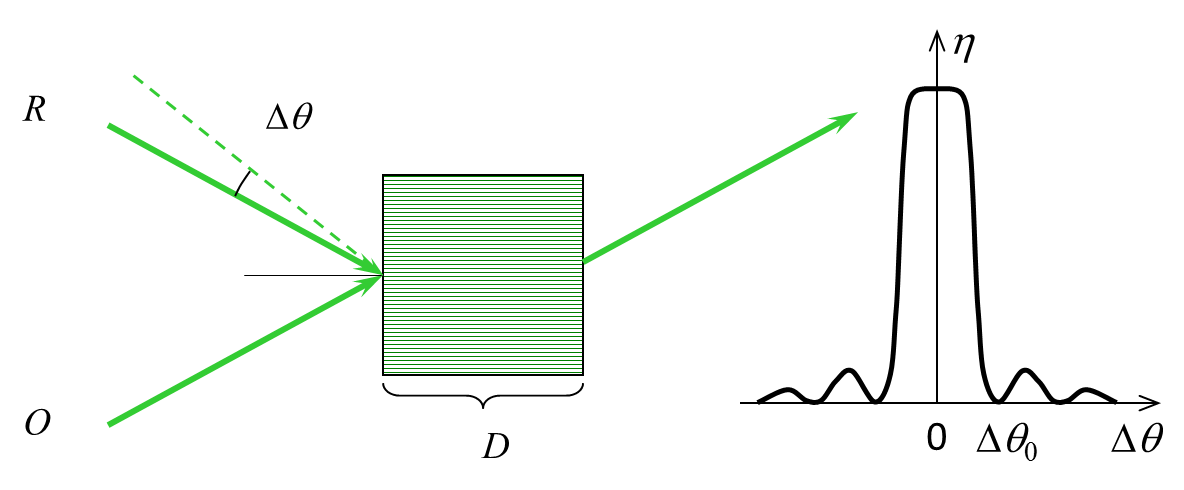
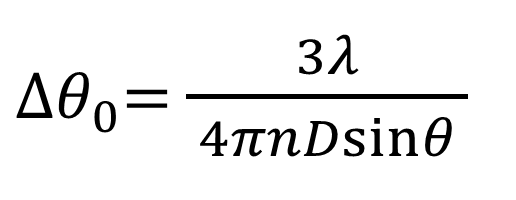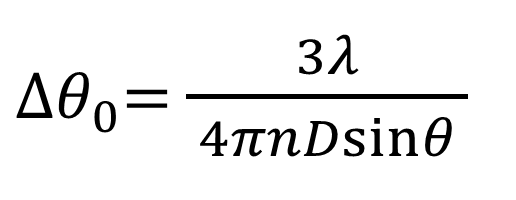全息可以简化成图1中所示的立体光栅。当参考光(R )按照布拉格角入射时，会衍射出再现的物光(O )。当参考光入射方向与布拉格角偏离量大于
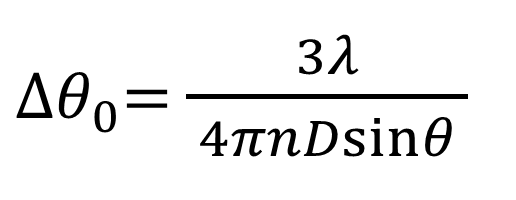再现的物光强度会急剧下降，发生布拉格失配现象，如图1右面的曲线。全息光存储就是利用布拉格失配这一特性，通过各种复用技术来获得高密度的信息存储。
|
|
|
Fig.1 Hologram is a volumetric grating.
|
|
下面介绍几种常用的复用技术。为了便于说明，我们采用k 矢量的来描述全息存储的各种复用技术。关于k 矢量的详细内容可参见体光栅的矢量描述。
|
|
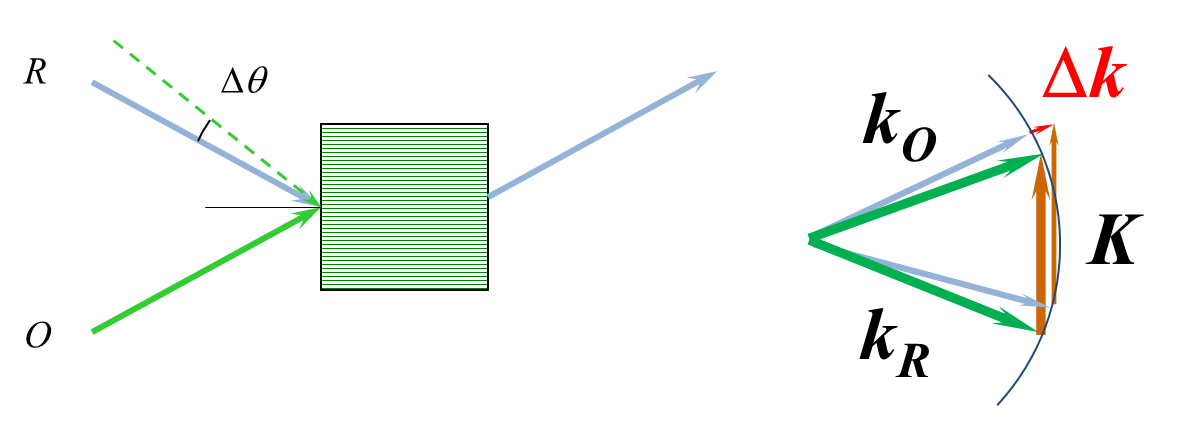
角度多重复用技术是直接利用布拉格失配原理来提高信息存储密度的。如图2所示，当参考光偏转角大于 Dq0 时衍射效率会急剧下降，在此再写入另一张全息图，在再现的时候，就不会相互干扰，实现多重记录，提高存储密度。光矢量图表示，当绿色的光波矢量记录的全息图 K 用蓝色的光波矢量再现时，无法构成一个封闭三角形，存在一个 Dk 的矢量差。
|
|
Fig.2 Angle multiplexing
|
| |
波长多重复用技术是利用波长的变化实现布拉格失配，从而提高信息存储密度的。如图3所示，当参考的波长改变 Dl 时衍射效率也会急剧下降，因此再写入另一张全息图，在再现的时候，就不会相互干扰，实现多重记录，提高存储密度。光矢量图中表示，当绿色的光波矢量记录的全息图 K 用蓝色的波长不同的光波矢量再现时，无法构成一个封闭三角形，也会产生一个 Dk 的矢量差。
|
|
|
Fig.3 Wavelength multiplexing
|
|
|
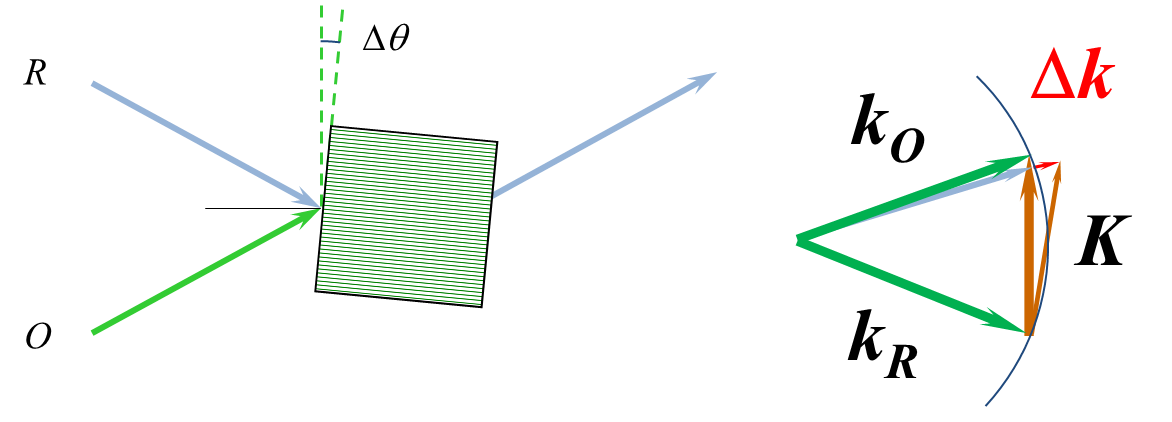
存储介质旋转多重复用技术与角度复用原理相同，它是通过旋转 K 来实现布拉格失配，以提高信息存储密度的。如图2所示，当存储介质旋转 Dq 角后，再写入另一张全息图，在再现的时候，就不会相互干扰，实现多重记录，提高存储密度。光矢量图表示，当光栅矢量 K 旋转之后，同样的光波矢量再现时，无法构成一个封闭三角形，会有一个 Dk 的矢量差。
|
|
Fig.4 Rotating multiplexing
|
|
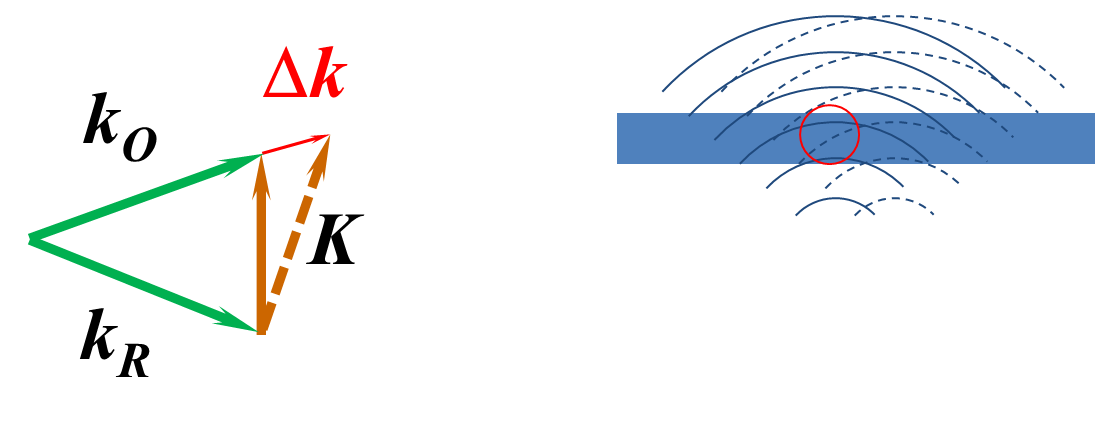
平移多重复用技术是间接利用角度复用原理，要求参考光必须是球面光波，当球面光波平移一定距离时，相当于参考光矢量 kR 移到了不同的光栅矢量 K 处，达到布拉格失配的效果，如图5所示，红圈中的实线和虚线的波面是不平行的。在此位置再写入另一张全息图，在再现的时候，就不会相互干扰，实现多重记录，提高存储密度。光矢量图表示，平移之后光栅矢量 K 发生旋转，同样的光波矢量再现时，无法构成一个封闭三角形，会有一个 Dk 的矢量差。
|
|
|
Fig.5 Shift multiplexing
|
|
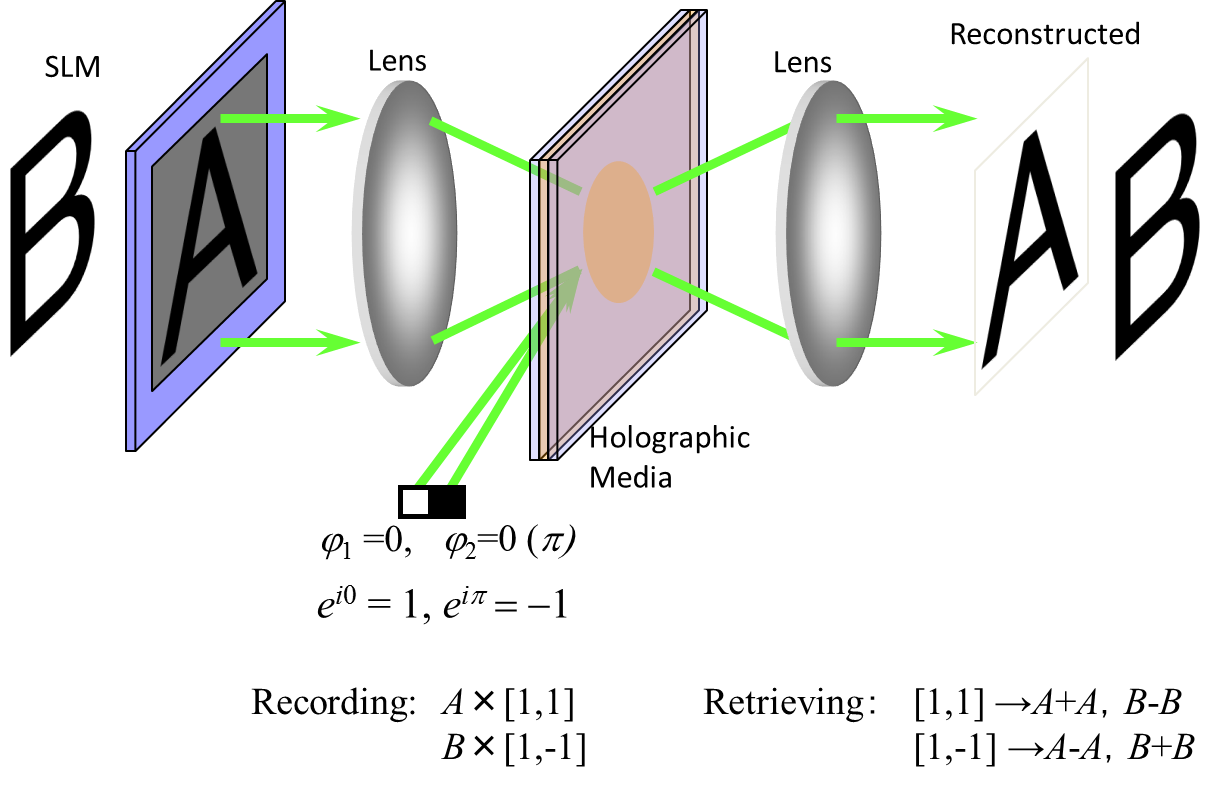
相位调制多重复用技术是利用相位的正交性对参考光进行编码，通过正交编码实现提高信息存储密度的，如图6所示。将两个相位调制器看作两束参考光，当 j1 与 j2 取相同相位 0 时，存储“A”字；当 j1 与 j2 分别取 0 和 p 相位时，存储“B”字。再现时，如果用相同的 0 相位的参考光入射，此时，两束参考光分别再现出两个“A”字和“B”字。由于“A”字是在相同相位的条件下记录的，因此再现出来的两个“A”字也是同相位的；可是“B”字是用相位差为 p 的两束参考光记录的，因此，再现出来的两个“B”字也带有 p 的相位差。其结果是“B”字相互抵消掉了，只剩下了“A”字。反之，如果用 0 和 p 相位的参考光入射，此时，两束参考光分别再现出的两个“A”字是有 p 相位差，而两个“B”字没有相位差。其结果是“A”字相互抵消掉了，只剩下了“B”字。在这里，我们采用的两束参考光分别加以 0 和 p 的相位调制，这种调制所采用的编码就是正交码。
|
|
|
Fig.6 Phase modulation multiplexing
|
|
在全息光存储的相位复用技术中，复用的数量取决于正交码的维数。如图7所示，列举了几个多维正交码。
|
|
|
Fig.7 Phase modulation multiplexing
|
|
