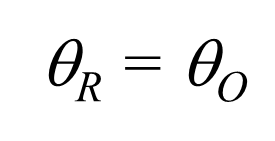
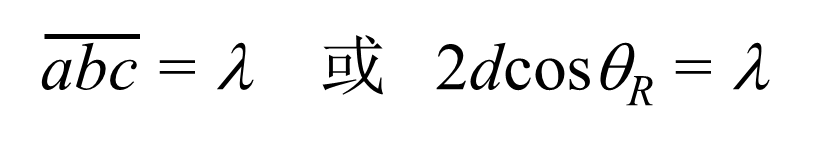
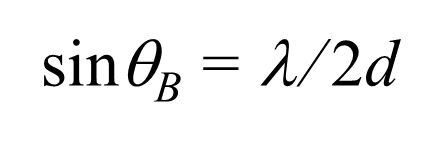
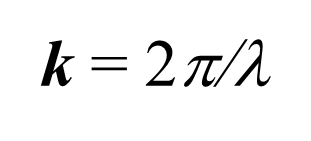

wave vectors
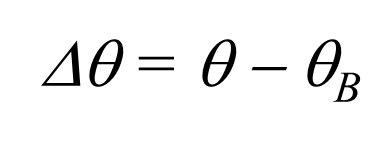
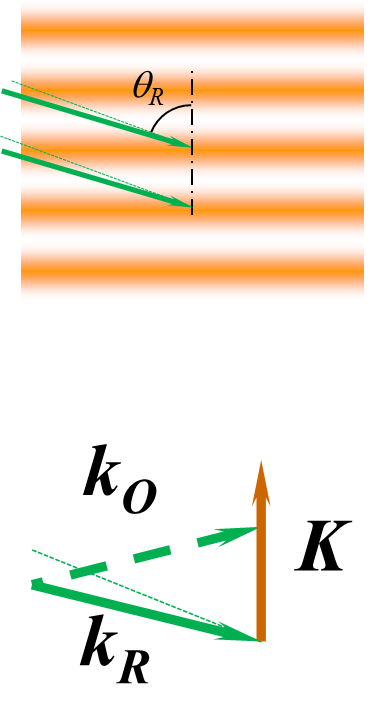
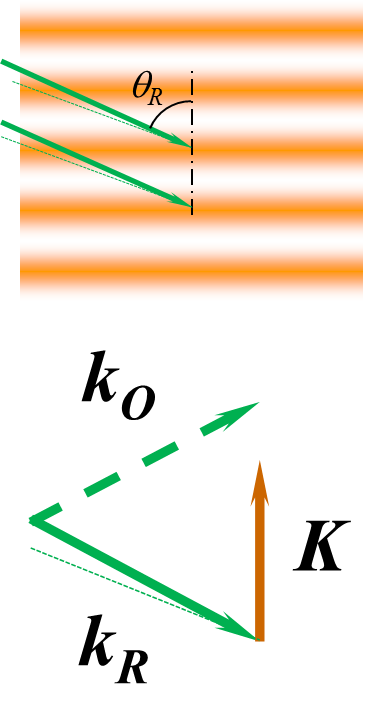
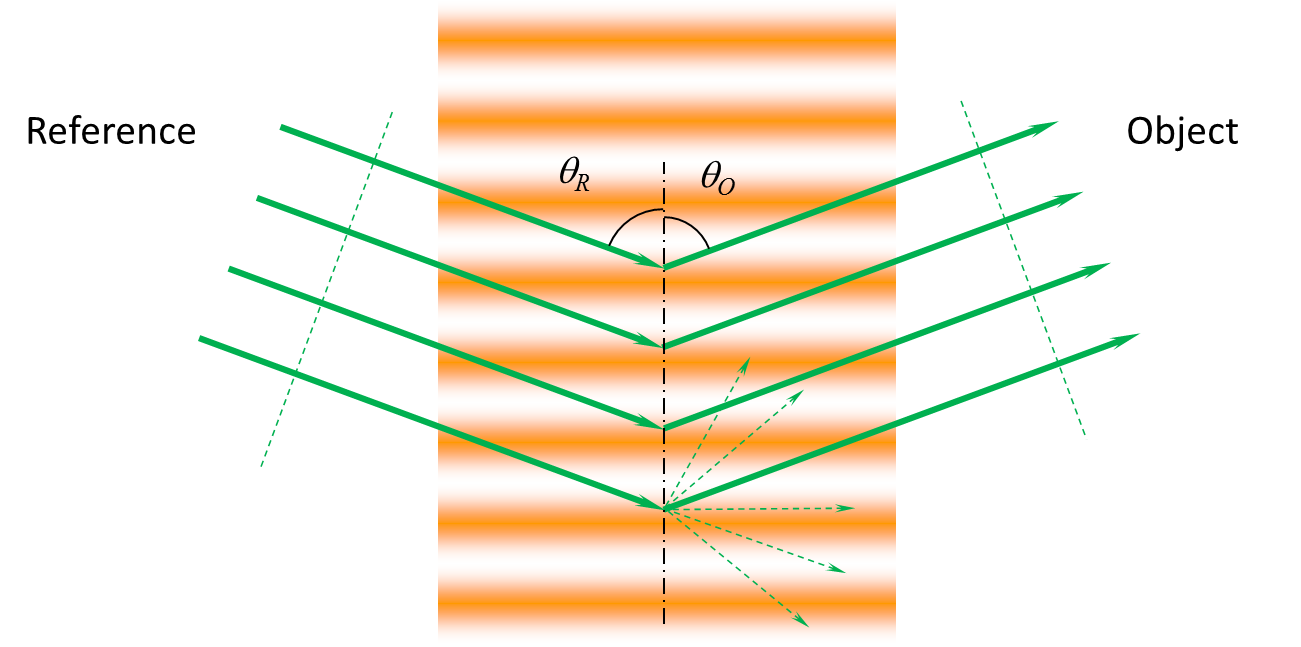
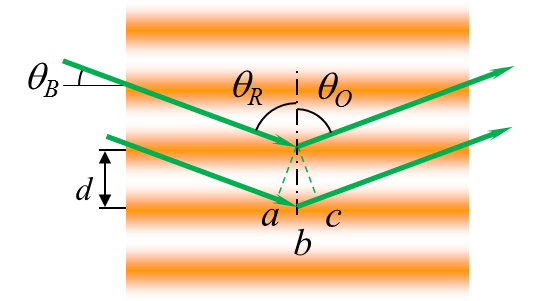
| 全息记录是将两光束的干涉条纹图案即明暗分布转换成材料的折射率或透射率变化来实现的。这种具有折射率或透射率变化的记录载体可以简化成图1中所示的立体光栅。这种光栅被再现参考光(Reference)照射之后,由于折射率或透射率变化导致的不均匀性,使得入射光在其内部发生散射,但是这些散射光只在某个(或某些)方向上才产生较强的衍射光。这个衍射光就是被记录下来的物光(Object)。能产生衍射光极大的条件,我们称之为布拉格条件。 |  |
||
| Fig.1 Hologram is a volumetric grating. | |||
在满足布拉格条件时,再现参考光(Reference)的必须满足: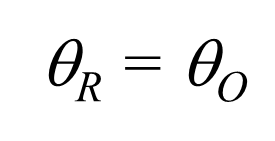 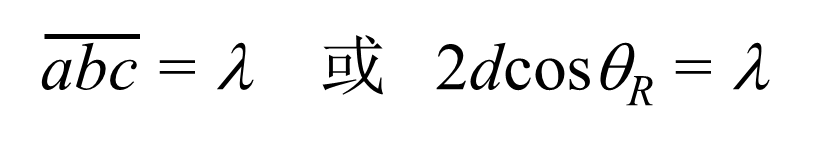 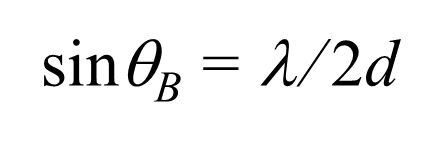 |

|
||
| Fig.2 Bragg condition | |||
为了说明问题的方便,通常将具有周期性的光波和光栅分别用下面的矢量表示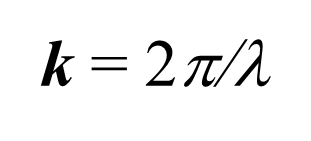  |

|
||
|
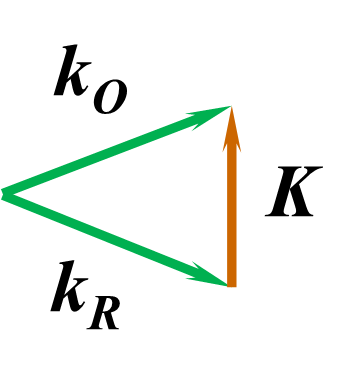
Fig.3 Bragg condition by wave vectors |
|||
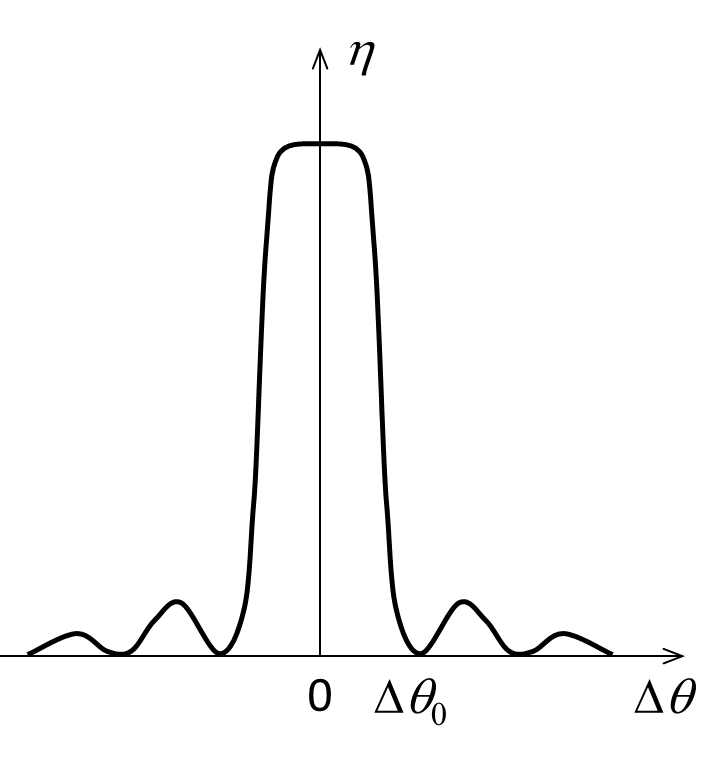
当参考光 kR 的入射方向不满足布拉格条件时, kO 、 kR 和 K 这三个矢量就无法构成一个封闭的三角形。图4分别表示了参考光的入射角大于和小于布拉格角时的情形。图4中间的曲线表示光栅衍射效率与入射角的变化规律,其中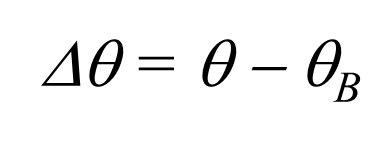 |



|
||
| Fig.4 Off Bragg condition. | |||
