李正煜同学在偏光全息原理研究中获得新进展
在基于张量描述的偏光全息理论中,A 和 B 是光场导致的介电张量变化的标量部分和张量部分的系数。它们将显著地影响再现光偏振态的变化,准确地测量其变化对制作偏振光学器件至关重要。我们提出了一种新颖且高效的方法来分别测量标量和张量部分的系数 A 和 B,并获得重要的 A/B 值。该方法避免了光束干涉角的影响,简化其实验过程。与以往的方法不同,所记录的全息图的偏振状态可以是任意极化的,这极大地提高了该方法的实用性。此外,所提出的方法采用了一个直接的分析过程,允许通过 p 和 s 偏振分量的光强直接观察系数 A 和 B 各自的变化。 |
|
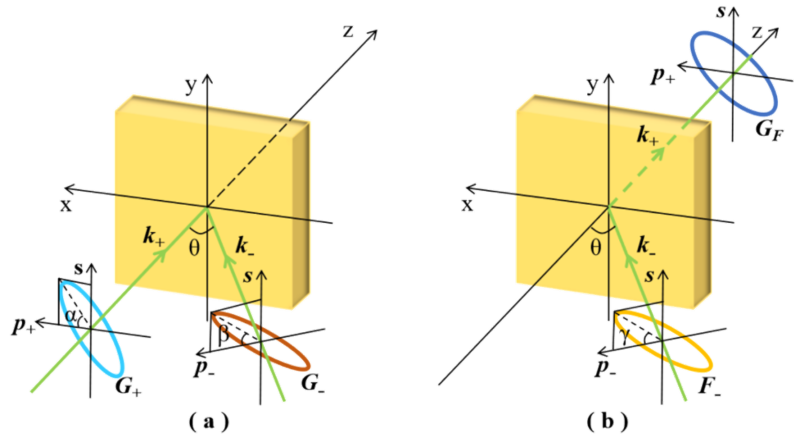
| 图1 偏光全息示意图。(a)记录过程;(b)读取过程 |
偏光全息的记录过程和读取过程如图1 所示。其中,G+、G-、F-、GF 分别表示信号光、参考光、读取光和再现光,θ 表示材料内部信号光与参考光之间的干涉角。α、β、γ 分别为信号光、参考光和读取光的偏振角,表示 s 和 p 分量振幅比的反正切值。将任意偏振态的信号光、参考光和读取光表达式代入基于张量描述的偏光全息理论中再现光的表达式,我们可以得到更一般的表达式。在该表达式中,再现光由 p 和 s 偏振分量组成,它们分别受参数 α、β、γ 和 θ 以及系数A和B的影响。为了便于观察系数 A 和 B 的变化,我们通过设置约束条件,让再现光的 p 和 s 偏振分量中仅存在系数 A 或 B。最后,通过求解这些约束条件,我们得到测量系数 A 和 B 的理论条件如表1 所示。 |
表1 测量系数 A 或 B 的理论条件 |

|
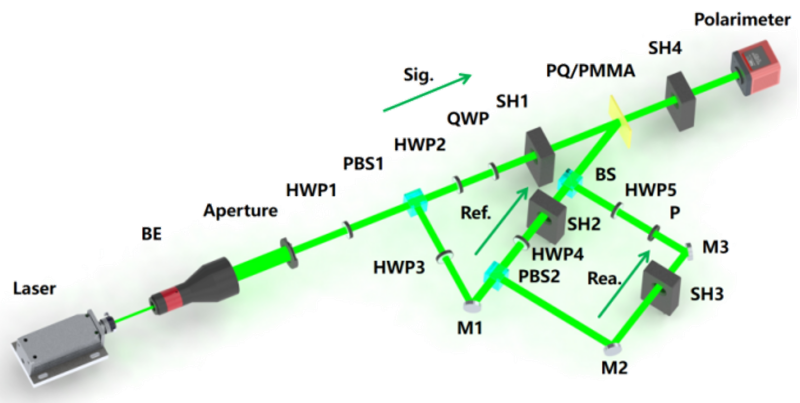
利用表1 中的条件,我们设计 6 组不同的实验分别对线偏振、椭圆偏振和圆偏振记录条件下的系数 A 或 B 的变化进行测量。实验装置如图2 所示,将波长为 532nm 的激光扩束成直径为 5mm 的平行光束。这束光通过偏振分束器(PBS1)被分成两束:一束作为信号光,另一束被 PBS2 进一步分成参考光或读取光。HWP1 和 HWP3 用于确保信号光、参考光和读数光的光功率相同。信号光的偏振状态由半波片(HWP2)和四分之一波片(QWP)控制,而参考光或读取光的偏振状态则通过旋转 HWP4 或 HWP5 来调整。 |
|
| 图2 实验装置示意图 |
|
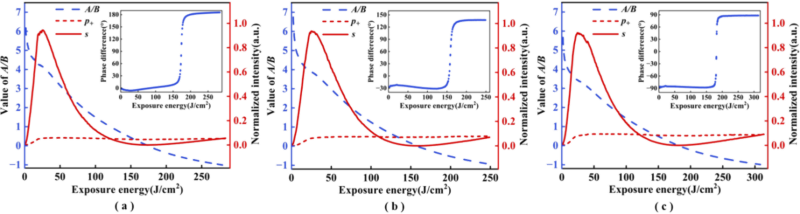
| 图3 情况 I 中 p+ 和 s 分量的归一化强度、A/B 值以及 p+ 和 s 的相位差随曝光能量的变化。(a)线偏振(φ=0°);(b)椭圆偏振(φ=30°);和(c)圆偏振(φ=90°) |
|
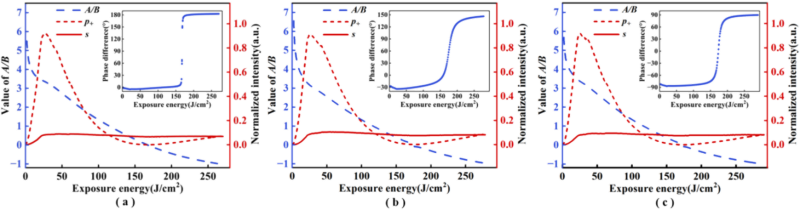
| 图4 情况 II 中 p+ 和 s 分量的归一化强度、A/B 值以及 p+ 和 s 的相位差随曝光能量的变化。(a)线偏振(φ=0°);(b)椭圆偏振(φ=30°);和(c)圆偏振(φ=90°) |
实验结果如图3 和 4 所示,在不同偏振记录条件下系数A和B的变化基本一致,A/B 从初时正值随着曝光能量的增加先快速后缓慢的下降到 -1。在情况I中,p+ 偏振的分量只与系数 B 相关,s 偏振的分量只与系数 A 相关,而在情况 II 中则是相反。因此,我们可以看到图3 中 p+ 偏振分量光强的变化曲线与图4 中 s 偏振分量光强的变化曲线一致,而图3 中 s 偏振分量光强的变化曲线与图4 中 p+ 偏振分量光强的变化曲线一致。我们还注意到表征系数 A 变化的偏振光强出现了先降低到接近 0 后又逐渐增加的变化过程,并且 p+ 和 s 的相位差在光强为接近 0 时出现了 π 左右的变化,这意味 A/B 在从正值下降为负值的过程中是系数 A 的符号发生改变。 我们的工作进一步证明,A/B 比值的变化主要受曝光能量的影响,而对所记录的全息图的偏振状态的依赖性较小。对标量和张量系数的独立测量和动态观测有助于更好地理解它们的变化特性,并有望于帮助针对不同应用的先进光学器件的制造。 |
上述研究成果以“Independent measurement and dynamic observation of scalar and tensor coefficients in polarization holography”为题,整理发表在美国光学学会 (The Optical Society of American, OPTICA) 期刊杂志 Optics Letters, Vol.50, No.7, 1-4 (2025)上。 论文的相关链接:https://doi.org/10.1364/OL.558178 |

|
(2025.03.17)
