郑淑君同学在偏光全息应用研究中取得新进展
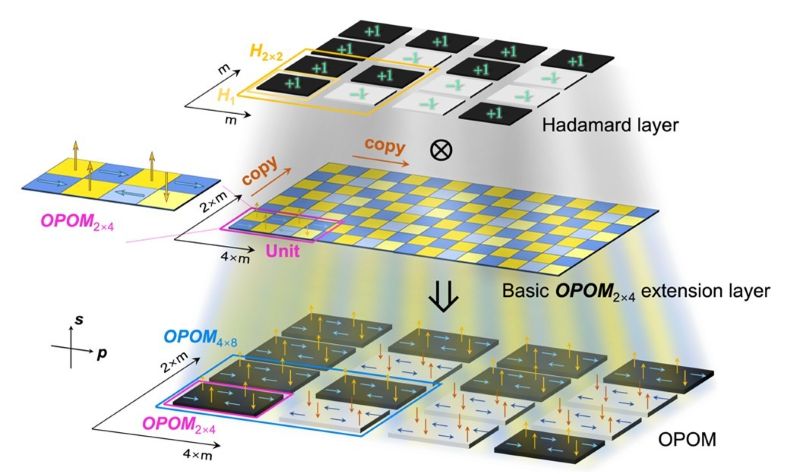
多路复用技术作为一种有效提升信息存储与传输能力的手段,一直备受关注。然而,在探索各种维度的多路复用技术时,偏振维度因其有限正交组合的局限性而面临挑战。鉴于在基本的庞加莱球面上仅能识别出两个相互正交的偏振状态,这无疑对偏振调制构成了极大的障碍。为克服这一难题,我们提出了一种光学偏振正交矩阵(OPOM)的构造方法,该方法成功突破了正交组合数量的限制。此外,我们还通过实证研究验证了该方法在偏光全息高维多路复用中的应用效果。 我们深入探索了偏光全息技术,该技术能够同时记录振幅、相位和偏振信息,旨在实现偏振多通道的记录与选择性重建。研究结果显示,尽管偏振状态相同,但由于信息间具有正交选择性,多个图像仍可在不同的偏振通道内通过正交偏振组合实现独立操作。通过选择所需的输入偏振状态组合,重建的图像能够在几乎无串扰的情况下进行切换。这种由偏振单元向量构成的非方形矩阵,为多通道信息检索和动态显示提供了广阔的前景,并在光通信、光学存储、逻辑设备、防伪以及光学加密等领域展现出潜在的应用价值。 在构造任意OPOM之前,我们首先推导出了最小 OPOM,即 OPOM2×4,具体推导过程可详见偏光正交矩阵的相关内容。如图1 所示,在构建基本的 OPOM2×4 扩展层时,我们以 OPOM2×4 为最小单位,通过复制边长为 m 的矩形来生成扩展层。同时,我们还构建了 Hadamard 层,该层是通过排列 Hadamard 矩阵的元素而形成的。Hadamard 层中的元素模块与基本 OPOM2×4 扩展层中的元素一一对应并相乘,从而生成 OPOM。图1 中给出了一个具体的例子,其中 OPOM4×8 是通过将 H2×2 与基本 OPOM2×4 扩展层的相应位置元素相乘而得出的。按照此扩展规律,我们可以得到 2m×4m 的OPOM(m 为正整数)。 |
|
| 图1 OPOM 的构造关系图 |
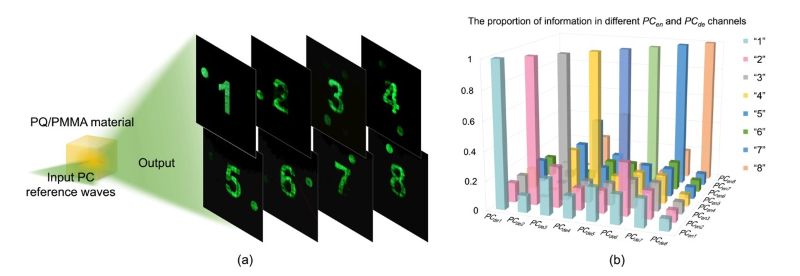
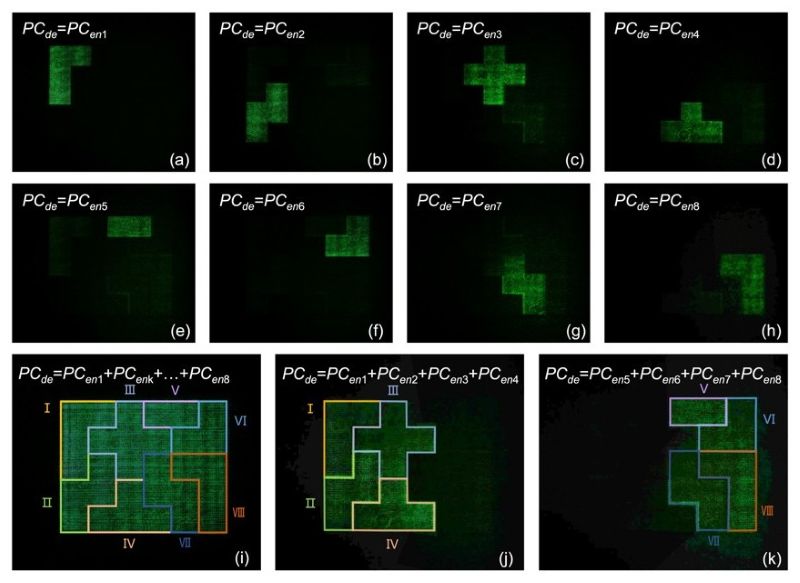
在本项工作中,我们充分利用了偏光全息在 90 度干涉夹角下具备正交零再现的特性,使用 OPOM4×8 的 8 组列向量作为偏振密钥。在先后记录了 8 幅全息图后,我们再利用这 8 组密钥进行读取,成功实现了多通道数字信息的检索(图2)与图像的动态显示(图3)。 |
|
| 图2 使用 OPOM4×8 实现数字信息检索的实验结果 |
|
| 图3 使用 OPOM4×8 实现图像动态显示的实验结果 |
我们的 OPOM 概念的提出不仅具有创新性,还为光通信、多维光学存储、光学逻辑设备、防伪以及超高安全性光学加密等多通道广播应用开辟了新的可能性。这项工作对正交矩阵领域做出了重大贡献,并有望推动这些领域的进一步研究和发展。 |
上述研究成果以“Optical polarized orthogonal matrix”为题,整理发表在光学一区 Top 期刊 Photonics Research, Vol.13, No.2, 373-381 (2025) 上(IF=6.6)。 论文的相关链接:https://www.researching.cn/Articles/OJ11b972e6a6c6946c |

|
(2025.01.28)
