郝建颖同学将深度学习应用在全息存储中取得新进展
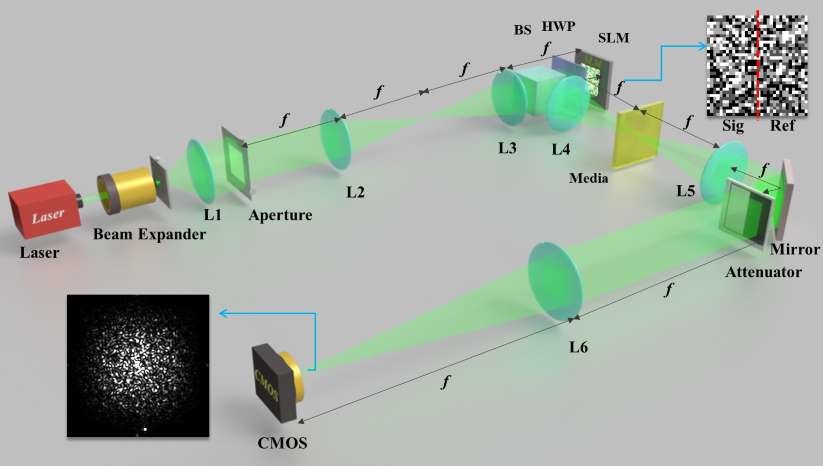
相位型全息存储,利用光的相位对信息数据进行编码,提高了全息存储的单页存储密度和信噪比。由于相位信息不能被直接探测,需要从探测强度图中计算得到编码相位信息。一种方法是利用傅里叶透镜将包含相位信息的重建光转化为傅里叶频谱面,并通过迭代傅里叶变换的方法进行相位计算。该方法通过CCD拍摄的单幅傅里叶图像即可重建获得相位编码图像,系统简单稳定。但是由于系统噪声的存在,会出现傅里叶面图像质量退化而降低相位解码精度。 郝建颖提出将深度学习应用于相位型全息存储中并获得高精度相位重建的方法。通过学习模拟的傅立叶面强度图像与真实实验捕获强度图像之间的相关关系,利用神经网络对捕获的图像进行降噪。之后使用迭代傅里叶变换算法(IFTA)对降噪后傅立叶强度图像进行相位恢复。实验系统如图1所示。 |
|
| 图1 迭代傅里叶变换同轴相位重建系统实验原理图 |
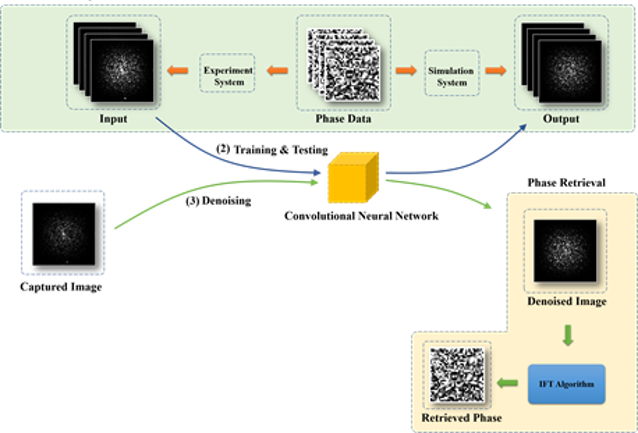
实验流程如图2所示,包含:(1) 数据集准备。搭建相位型同轴全息存储仿真和实验系统。生成4灰阶随机编码数据页并计算仿真傅里叶面图像。上载编码数据页到实验系统,并拍摄实验傅里叶面图像。(2) 神经网络训练。 将实验图像作为输入,仿真图像作为输出(真值)输入卷积神经网络(CNN)系统进行训练和泛化验证。 (3) 去噪和相位重建。对于新的傅里叶面图像,先输入训练后的CNN进行降噪,然后利用迭代傅里叶变换算法(IFT)进行相位重建。 |
|
| 图2 傅里叶面降噪与相位解码流程图 |
实验解码图像以及误码分布状况如图3所示,图中白色点表示误码。实验结果表明,与直接解码捕获的图像相比,使用卷积神经网络进行降噪后,相位解码误码率显著降低。 |

|
| 图3. (a) 实验解码结果,(b) 实验拍摄图像,(c) 相位直接重建,(c) 重建相位误码率, (e) 降噪后的图像,(f) 降噪图像后的重建结果,(g) 降噪后重建相位的误码率 |
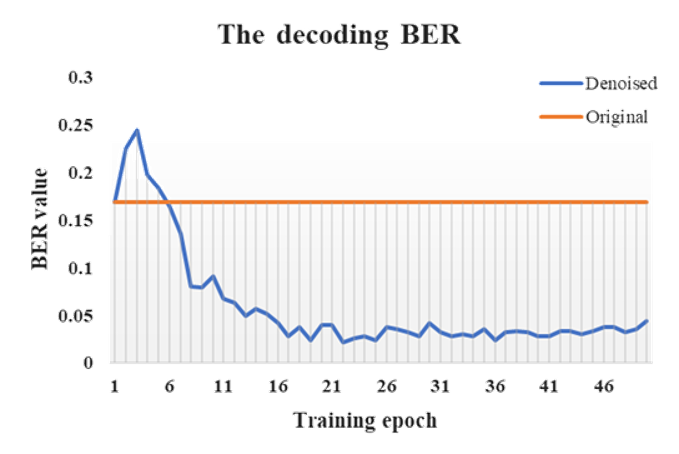
训练过程误码率如图4所示,图中实验拍摄图像的解码BER如橙色线所示,值为0.168。 随着训练轮数的增加,误码率逐渐趋于收敛。 经过训练后的神经网络去噪,相位解码的误码率平均可以降低到0.025左右。 |
|
| 图4. 深度学习降噪图像与直接拍摄图像误码率对比 |
综上,提出了一种基于深度学习降噪的相位重建方法。通过实验验证,与IFTA直接进行相位重建相比,利用深度学习降噪后的图像进行解码,误码率降低了6.7倍,验证了深度学习在相位调制全息存储中提高相位重建精度的可行性。 相关研究的结果以“Phase retrieval combined with deep learning denoising method in holographic data storage”为题,整理发表在美国光学学会(The Optical Society of American, OSA)期刊杂志 Optics Continuum, Vol.1, No.1, 51-62 (2022)上。 论文的相关链接:https://doi.org/10.1364/OPTCON.444882 |

|
(2022.01.12)
