林枭同学在全息光存储研究中取得新进展
相位型全息数据存储以其更高的存储密度和更高的信噪比特点成为了最近光学数据存储的研究热点。但是相位无法直接被探测器读出,通常需要与另一束相位读取参考光进行干涉,将相位转化成强度分布,再由探测器测出。但是干涉系统不但更为复杂,而且稳定性差,不利于全息数据存储。 林枭等人通过结合迭代傅里叶变换算法,更是加入了特有的嵌入式数据编码,提出一种快速非干涉相位重建方法。该方法不仅系统简单、稳定,而且在全息数据存储中发挥了其编码可控的特有优势,使得本来需要成百上千次的循环计算一下子减少到个位数循环计算,使之成为实际可用的方法。 |
|
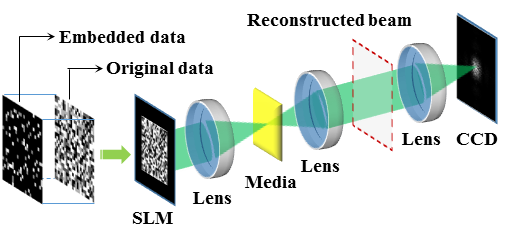
Fig. 1. The diagram of non-interferometric system for phase retrieval. |
图1显示了该方法的系统简图,只需要在重建光后加一个透镜,将傅里叶强度记录下来即可。 表1显示分别显示了4阶相位和8阶相位的重建情况。在使用50%嵌入式数据的情况下,通常只需要十次左右的循环次数就可得到可接受的误码率,而且此时编码率较振幅式编码有了两到三倍的提升。 |
| Table 1. Simulation results for 4-level phase and 8-level phase encoding for different proportions of embedded data |
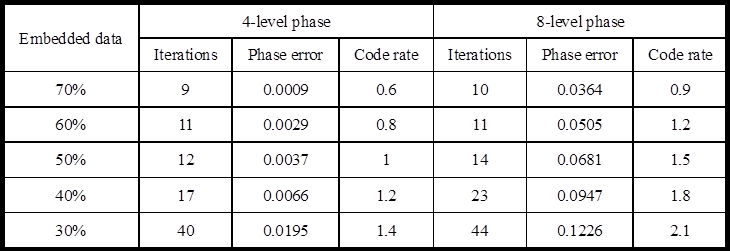
|
为了验证该方法的可行性,将一副灰度图进行编码并利用全息数据存储系统进行存储,并读取还原出灰度图。编码过程如图2所示。灰度图先分成若干个小的部分,每部分编码成一个4阶相位矩阵,其中包含50%的嵌入式数据。然后将这些相位矩阵进行全息存储。 读取数据时,先将各个相位矩阵中的相位按照非干涉法进行重建,然后再恢复原灰度图。恢复结果如图3所示。其中图3(a)表示原图,图3(b)表示直接进行相位重建后的恢复图,图3(c)表示利用非干涉法迭代10次相位重建后的恢复图。从图中可以看出,运用本方法后,恢复图的质量明显变好,误码率可以控制在5%左右。在加入适当的校验码后,可以将误码率降为0。 |

|
Fig. 2. Illustration of the process of encoding gray image to phase patterns to be recorded. Images of 128×128 pixels is divided into sub-blocks of 32×16 pixels first. Then encoding phase data with 64×32 pixels are generated as 4 phase pixels are used to encode a single image gray value. A fixed known embedded phase data page with 64×32 pixels is combined with the encoding phase data to form the 64×64 phase pattern. Then every pixel of the 64×64 phase pattern is enlarged by a 8×8 block to form the final 512×512 phase pattern uploaded on the SLM. Combination rules of the encoding phase and embedded phase is illustrated in the dashed line rectangular. (Pixels with north-east direction texture represents embedded phase data positions and pixels with north-west direction texture represents encoding phase data positions.) |

|
| Fig. 3. Test image (a) Original image, (b) Reconstructed image based on initial guess, (c) Reconstructed image based on resolved phase after 10 iterations. |
基于以上研究,以“Fast non-interferometric iterative phase retrieval for holographic data storage”为题目的论文,已被Optics Express(影响因子:3.307)接收,并发表在:Vol. 25, Issue 25, pp. 30905-30915。 论文的相关链接:https://doi.org/10.1364/OE.25.030905 |

|
(2017.11.28)
