范荣铨同学在全息存储研究中取得新进展
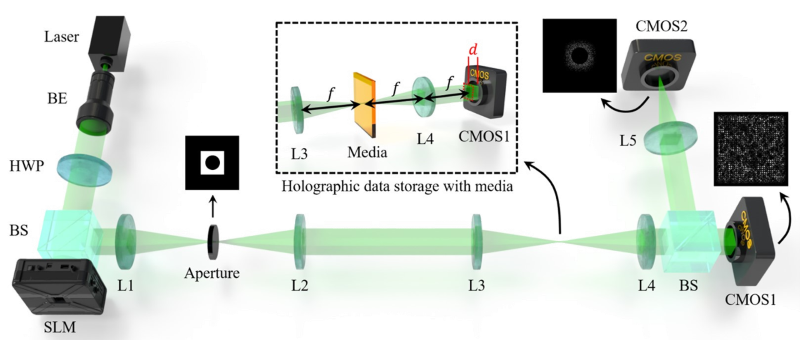
全息光存储技术是一种将二维信息保存在三维立体空间中的存储技术,其具有存储密度高、存储寿命长等特点。相位调制型全息存储技术有着较高的编码率和信噪比,成为近年来的研究热点。在之前的研究中,我们利用端到端卷积神经网络建立已知编码数据页与其近场衍射强度之间的关系,从而预测未知相位数据页。由于网络模型的训练效率主要由相邻相位的边缘决定,这意味着我们可以选择性记录对训练有增益的频率。 本文提出了一种深度学习与带通滤波相结合的相位重建方法,仅记录相位图像的部分频率分量并进行深度学习训练,即可实现相位检索。我们对相位图的低频分量进行衰减,分析能够滤波的频率范围。此外,为了消除高级次频率分量带来的噪声,我们滤除两倍奈奎斯特间隔以上的频率,实现了相位图的带通滤波。实验结果表明,该方法可以减少介质消耗,提高存储密度。 实验系统如图1 所示。图中的光阑作为滤波器来调节信息光的空间频率分布。在记录过程中,将编码好的相位数据页加载到空间光调制器上作为信息光,信息光与另一参考光发生干涉,在存储介质中形成全息图。在读取过程中,用相同的参考光照射全息介质,产生一束衍射光,实现对信息光的再现,称为重建光。让重建光在自由空间中继续传播一小段距离,利用图像探测器捕获衍射强度图像。 |
|
| 图1. 相位调制型全息存储实验系统 |
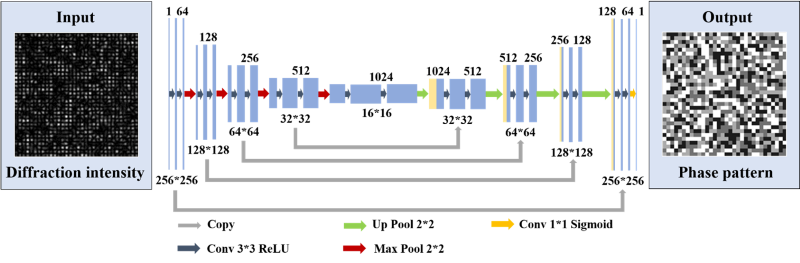
本文采用 4 灰阶相位编码 (π/6, 2π/3, π, 3π/2), 6000 对图像作为训练数据集,1000 对图像进行测试数据集,10 对图像用于验证数据集。U-net 卷积神经网络架构如图2 所示。使用 CMOS 捕获的衍射强度图像作为神经网络的输入,以相同大小的相位数据页作为输出。 |
|
| 图2. 卷积神经网络架构 |
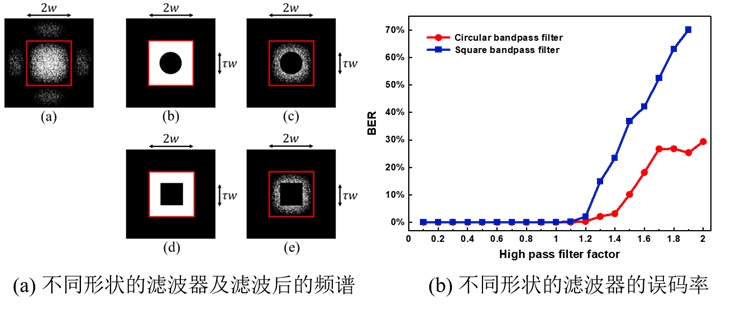
我们将滤波器的下阻带尺寸定义为高通滤波因子。在模拟中分析两种滤波器在不同高通滤波因子下的误码率,如图3(b) 所示。当高通滤波因子值大于 1.1 时,圆形带通滤波器的相位重建效果优于方形带通滤波器,因为圆形带通滤波器的频率响应比方形带通滤波器更平滑,可以更好地保留图像中的边缘信息,避免锐化效应和边缘模糊。因此,在后续的实验中,只使用圆形带通滤波器。 |
|
| 图3. 不同形状的带通滤波器对比 |
在实验中,为了抑制动态噪声的影响,我们对数据进行了打乱处理。当高通滤波因子为大于 1.8 时,系统噪声与重建光的强度基本一致,导致探测器很难获取相应强度的图像。实验与仿真中高通滤波因子与误码率的曲线关系如图4(b) 所示。由于衍射强度随着高通滤波因子的增大而减弱,放大了相机动态噪声对重建效果的影响。相反,由于模拟中没有加入噪声,因此可以对衍射强度进行归一化,增强了其较暗的高频细节,使得相位恢复相对稳定。当不添加校验码时,我们认为在相位调制型全息存储系统中,误码率在 0.1% 左右是可以接受的。因此,确定最佳的高通滤波因子为 0.9,误码率为 0.1%。经过带通滤波后,记录的光强仅为未滤波时光强的 33.97% 左右,能够节省存储介质约 2.94 倍。 |

|
| 图4. (a) 不同高通滤波因子的材料节省倍数;(b) 实验中不同高通滤波因子的误码率 |
本研究提出了一种深度学习与带通滤波相结合的相位重建方法。通过仿真讨论了该方法的参数设置,并通过实验验证了该方法的可行性。该方法通过对信息光进行带通滤波,减少了存储介质的消耗,使存储容量提高了 2.94 倍。此外,该方法滤除两倍奈奎斯特间隔以上的频率,提高了系统的抗噪声能力,并且对衍射距离不敏感。同时,该方法对实验系统的透射率和孔径位置有较高的容忍度。 |
上述研究成果以“Phase retrieval based on deep learning with bandpass filtering in holographic data storage”为题,整理发表在美国光学学会 (The Optical Society of American, OPTICA) 期刊杂志 Optics Express, Vol.32, No.3, 4498-4510 (2024) 上。 论文的相关链接:https://doi.org/10.1364/OE.511734 |

|
(2024.01.25)
