邱仙颖同学在全息存储研究中取得新进展
全息光存储具有巨大的数据存储潜力,但是存储系统中的记录介质会发生尺寸变化,如遇到温度变化引起的收缩和体积变化,这会造成再现图像误码率升高,严重影响全息图的再现质量。传统的离轴系统中对记录介质尺寸变化的补偿是通过调整读取光束的入射角或波长来实现的,但由于其系统结构的复杂性,对振动很敏感,使得离轴系统中的补偿精度要求更高。相比之下,同轴系统更紧凑,稳定性更好,其对记录介质尺寸变化的补偿方式也有所不同。 为此邱仙颖等提出了一种通过同时调整同轴系统中读取光的波长和物镜焦距来补偿记录介质尺寸变化的组合补偿方法,并在高尺寸变化率(σ=1.5%)的条件下比较了其对横向尺寸和纵向尺寸的补偿效果。 图1是记录介质尺寸变化模型分析图,通过对该模型的分析,提出了补偿记录介质尺寸变化的方法。横向尺寸变化在图中是指沿x-y平面的变化,对应的横向尺寸变化率 σL,纵向尺寸变化是指沿z轴方向的变化,则纵向尺寸变化率 σV |

|
| 图1. 记录介质尺寸变化模型示意图 |
同轴系统中焦距补偿原理图如图2所示,空间光调制器上的参考光束和信息光束由聚焦物镜聚焦到记录介质中,入射到材料表面的所有光束的角度由聚焦物镜的焦距决定,例如在图2(a)中焦距 f1 对应 θ1,焦距 f2 对应 θ2。然后通过使聚焦物镜焦距增大或减小的方式来调整读出光束的入射角度,这样就能够实现从原理上补偿由于介质尺寸变化的布拉格失配,使再现光重新满足布拉格条件,减小再现图像误码率。 |

|
| 图2. (a)同轴系统中焦距补偿原理图,(b)同轴全息存储系统的简化光路 |
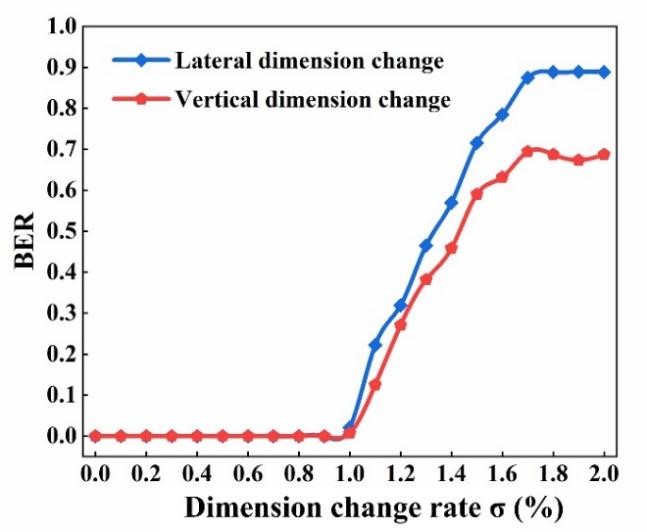
图3表示在没有任何补偿的情况下,横向或纵向尺寸变化条件下的再现图像误码率与不同尺寸变化率(σ)的关系曲线图。对于这两种维度的尺寸变化,当 σ 大于 1% 时,相应的误码率随着 σ 的增加而急剧增加。 |
|
| 图3. 尺寸变化率(σ)与误码率(BER)的关系 |
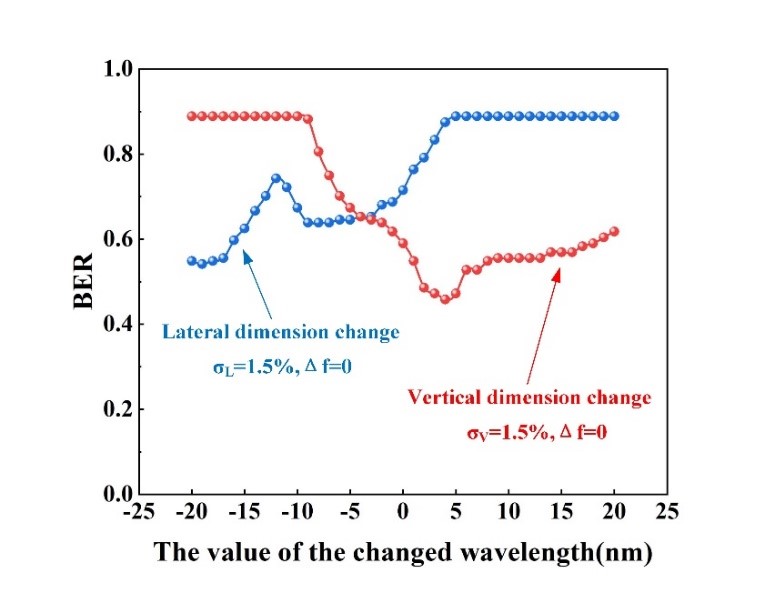
图4说明在横向和纵向尺寸变化条件下仅利用波长调整的补偿可以降低再现图像的误码率,但是在这两种尺寸变化情况下再现图像的误码率都不能降低到 0,补偿效果没有那么明显。 |
|
| 图4. 仅利用波长调整的补偿方法 |
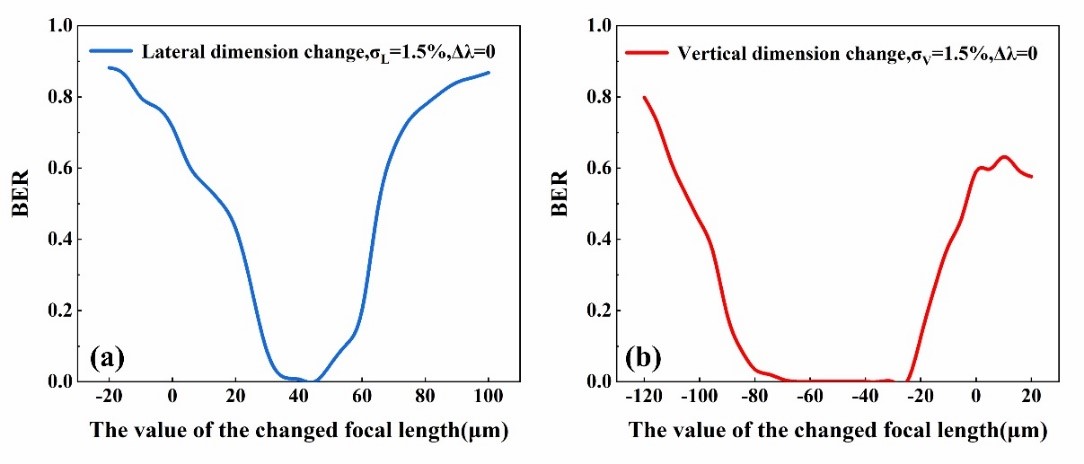
图5所示的是仅改变物镜焦距的补偿方法,其补偿效果明显优于波长补偿方法,并且在这两种尺寸变化条件下,误码率均可以降至 0。但是纵向尺寸变化条件下,误码率为0的焦距范围(约40μm)大于横向尺寸变化条件下的焦距范围(约5μm)。 |
|
| 图5. 仅改变焦距的补偿方法 (a)横向尺寸变化; (b)纵向尺寸变化 |
图6分析了在大范围内同时改变物镜焦距和波长的补偿效果,可以看出,无论是横向尺寸变化还是纵向尺寸变化,在高尺寸变化率 σ=1.5%下,实现零误码率补偿的波长和焦距的调整范围都比较大。 |

|
| 图6 波长和焦距的组合补偿方法 (a)横向尺寸变化; (b)纵向尺寸变化 |
综上所述,本文提出的波长和焦距的组合补偿方法相比于仅调整波长或焦距的补偿方法更有优势,可以扩大补偿范围,而较大的补偿范围有利于实验,该仿真结果可用于指导同轴全息存储系统的实现。基于该组合补偿方法取得的结果,同轴全息存储系统中记录介质的体积变化容限也将得到提高。 |
相关研究的结果以“Combination Compensation Method to Improve the Tolerance of Recording Medium Shrinkage in Collinear Holographic Storage”为题,整理发表在多学科数字出版机构(Multidisciplinary Digital Publishing Institute, MDPI)期刊杂志 Photonics. Vol.9, No.3, 149(11p) (2022)上。 论文的相关链接:https://doi.org/10.3390/photonics9030149 |

|
(2022.03.03)
