张伊盈同学在偏光全息理论研究中取得新进展
|
随着微纳材料和微纳光学理论研究的不断深入,近年来偏光全息理论也得到了进一步的发展。具有标志性进展的成果是2011年由我校兼职教授、日本东京大学名誉教授黑田和男(K. Kuroda)提出来的基于介电张量模型的偏光全息理论。这个新理论突破了之前的琼斯理论只能在两束相干光夹角非常小的条件限制,将两束全息记录用的信息光和参考光之间的夹角拓展到了三维空间。本研究室张伊盈同学的研究成果就是利用新偏光全息理论,在同研究室的吴安安和王珏两同学的研究成果的基础上再次取得的又一新成果。 按照琼斯理论,当振幅相同的两束分别为左、右旋的圆偏振光交汇时,根据琼斯理论得出的结果是:干涉出的偏振状态在空间呈不同方向的线偏振光的周期分布,如图1所示。这个结果显然只有在两束光近似平行的时候才可能出现。当两束光有一定夹角时这个结果是与实际不符的。实际的结果是各种椭圆偏振光的空间分布,如图2所示。基于黑田和男(K. Kuroda)教授的新理论则可精确地计算出与图2完全一致的结果。但是此理论只是一个粗犷的轮廓,还没有细致地论证和实验验证。 |

|
图1. 琼斯理论的计算结果 |
|
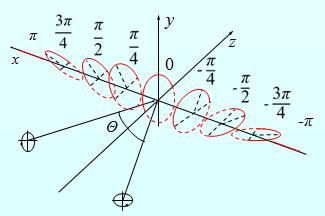
图2 实际的干涉结果 |
|
基于此张量理论,本研究室的吴安安同学经过理论计算和实验发现,如果将两个互为正交的圆偏振光的干涉条纹记录下来,再现时用正交的参考光再现时,只有在强度全息与偏振全息达到平衡时,会引起再现光消失的零再现现象。后来,王珏同学用实验验证了这一零再现出现的物理机理。为了探究更具有一般性的偏光全息理论,张伊盈同学开展了针对椭圆偏振光的记录和再现理论研究,并通过实验加以验证,取得了突破性的进展。 张伊盈同学经过系统的理论分析和计算,发现在强度全息与偏振全息达到平衡的条件下,椭圆偏振光也可以实现忠实再现。但是,当使用正交椭圆偏振光再现时,再现光与原信号光会有形状反转(如:扁椭圆变成竖椭圆),旋向不变的反转再现的现象。这一现象也在她本人设计并搭建的实验装置上反复多次验证了这一现象。从而在理论和实验上同时验证了椭圆偏振光的偏光全息再现特性。 基于以上研究,以“Inverse polarizing effect of elliptical-polarization recorded hologram at large cross angle”为题目的论文,已被Optics Letters(影响因子:3.041)接收, 并发表在:Vol. 41, Issue 17, pp. 4126-4129 (2016) 。 论文的相关链接: http://dx.doi.org/10.1364/OL.41.004126 |

|
(2016.09.01)
